Gene Set Analyses using Bayesian MAGMA Models

Peter Sørensen

Center for Quantitative Genetics and Genomics, Aarhus University, Denmark

Palle Duun Rohde

Genomic Medicine, Department of Health Science and Technology, Aalborg University, Denmark

From GWAS to Biological Discovery

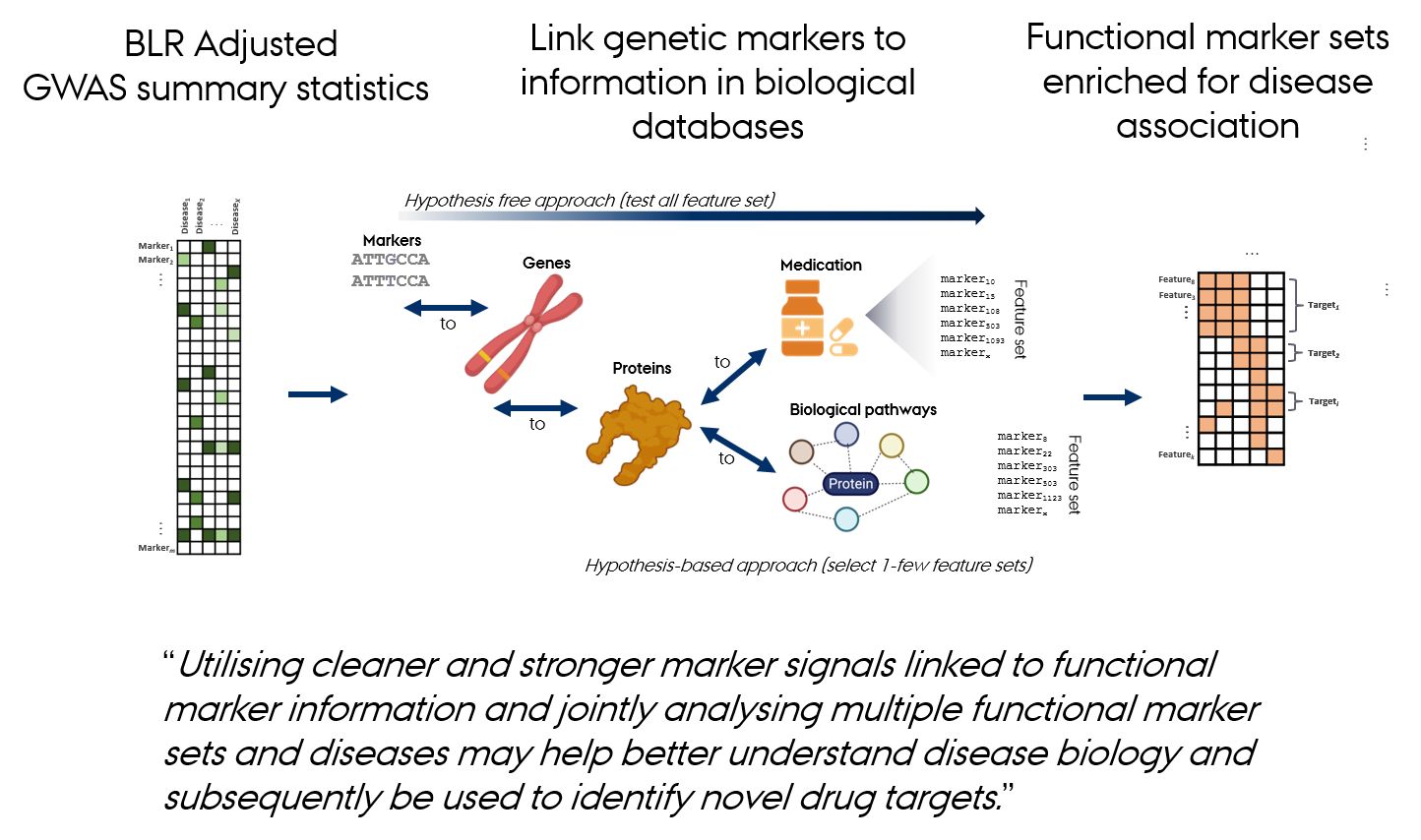
Gene Set Analysis

Gene set analysis evaluates the coordinated action of genes or sets of variants within predefined biological pathways or functional groups.

GWAS identify single genetic variants (SNPs) associated with traits or diseases.

Many variants have small individual effects
→ Use larger datasets or make better use of existing data.
Some effects are clustered within functionally related genes or pathways
→ Use prior information on functional marker groups to improve detection power and interpretation.
Some effects are shared across multiple traits
→ Leverage correlated trait information to enhance detection power and prediction accuracy.

Gene Set Analyses

Many different gene set analysis approaches have been proposed.

MAGMA: Multi-marker Analysis of GenoMic Annotation (Leuww et al 2015)
- generalized gene set analysis of GWAS data
- based on a multiple regression model
- rank gene sets
PoPS: Polygenic Prioritisation Scoring (Weeks et al 2023)
- leveraging polygenic enrichment of gene features (e.g. gene sets) to predict genes underlying complex diseases
- based on a multiple regression model
- rank genes

MAGMA: Linear Model Approach

MAGMA fits a linear regression model to test associations between gene sets and traits.

Aggregate SNP-level GWAS statistics into gene-level statistics, accounting for LD.
Use gene-level statistics as the response variable.
Represent gene sets as a predictor matrix, typically indicating gene membership, but not necessarily limited to binary values.
Estimate regression coefficients to assess the strength of association between each gene set and the trait.
Evaluate significance using permutation or model-based null distributions.

MAGMA: Limitations

When analyzing thousands of gene sets, several issues arise:
- Overfitting – the model may capture noise rather than true signals.
- Multicollinearity – many gene sets are correlated due to biological overlap.
- Multiple testing – increases false-positive risk.
- Interpretation difficulty – hard to disentangle contributions of overlapping sets.

→ Use of regularization and variable selection to improve model robustness and interpretability.

Additionally, many complex traits are genetically correlated, sharing overlapping biological pathways.

→ Incorporating multi-trait information in MAGMA can increase detection power and reveal shared genetic mechanisms across traits.

Bayesian MAGMA: Idea

Develop and evaluate a Bayesian gene-set prioritization approach using BLR within the MAGMA framework.

Advantages:
- Incorporates regularization and variable selection via spike-and-slab priors.
- Controls false positives and handles overlapping gene sets.
- Provides posterior inclusion probabilities (PIP) as evidence of gene set association.
Flexible framework supporting:
- Single- and multi-trait models
- Integration of diverse genomic features
- Modeling of correlated traits to uncover shared genetic factors.

Bayesian MAGMA: Regression Model

The Bayesian MAGMA framework builds on the standard regression model:

\[ \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}, \qquad \boldsymbol{\varepsilon} \sim \mathcal{N}(0, \sigma^2 \mathbf{I}) \]

$\mathbf{Y}$ — vector of observed outcomes or gene-/set-level association measures
$\mathbf{X}$ — matrix of genomic predictors (e.g., gene membership, functional annotations, or pathway indicators)
$\boldsymbol{\beta}$ — vector of effect sizes describing how predictors in $\mathbf{X}$ explain variation in $\mathbf{Y}$
$\boldsymbol{\varepsilon}$ — residual noise capturing unexplained variation

In the Bayesian formulation, each $\beta_j$ is assigned a prior distribution that encodes assumptions about effect size magnitude, sparsity, or functional grouping.
These priors enable regularization, variable selection, and information sharing across correlated features or biological layers.

Bayesian MAGMA: Multivariate Motivation

Traditional single-trait analyses may miss associations that are
weak individually but consistent across traits.
Multi-trait Bayesian MAGMA leverages these correlations by
jointly modeling multiple traits to:
- Increase power for detecting gene sets and pathways,
- Improve accuracy of effect estimation, and
- Reveal shared biological mechanisms underlying complex diseases.

Bayesian MAGMA: Multivariate Regression Model

In the multivariate BLR model, we model multiple correlated outcomes jointly:

\[ \mathbf{Y} = \mathbf{X}\mathbf{B} + \mathbf{E} \]

$\mathbf{Y}$: $(n \times T)$ matrix of outcomes
(e.g., association measures for $T$ traits or omic layers)
$\mathbf{X}$: $(n \times p)$ feature matrix
$\mathbf{B}$: $(p \times T)$ matrix of effect sizes
$\mathbf{E}$: $(n \times T)$ residual matrix

Each row of $\mathbf{Y}$ corresponds to an observation or gene, and each column to a trait, phenotype, or molecular layer.

Bayesian MAGMA: Error and Effect Priors

We extend the univariate priors to the multivariate setting: \[ \mathbf{e}_{i\cdot} \sim \mathcal{N}_T(\mathbf{0}, \boldsymbol{\Sigma}_e) \] \[ \mathbf{b}_{j\cdot} \sim \mathcal{N}_T(\mathbf{0}, \boldsymbol{\Sigma}_b) \]

$\boldsymbol{\Sigma}_e$: residual covariance among traits ($\mathbf{e}_{i\cdot}$ is the vector of residuals for observation $i$ across all $T$ traits)
$\boldsymbol{\Sigma}_b$: covariance of effect sizes across traits ($\mathbf{b}_{j\cdot}$ is the vector of effect sizes for feature $j$ across all $T$ traits)

When the off-diagonal elements are nonzero, the model borrows information across correlated traits, enabling detection of pleiotropic effects and shared genetic factors.

When $\boldsymbol{\Sigma}_e$ and $\boldsymbol{\Sigma}_b$ are diagonal, the model reduces to $T$ independent univariate BLR models.

Bayesian MAGMA: Indicator Variables

Each feature $j$ may affect multiple outcomes (traits).
We define an indicator vector for cross-trait activity patterns:

\[ \boldsymbol{\delta}_j = \begin{bmatrix} \delta_{j1} \\ \delta_{j2} \\ \vdots \\ \delta_{jT} \end{bmatrix}, \qquad \delta_{jt} = \begin{cases} 1, & \text{if feature $j$ affects trait $t$}, \\ 0, & \text{otherwise.} \end{cases} \]

After Gibbs sampling, the posterior inclusion probability (PIP) is estimated as:

\[ \widehat{\text{PIP}}_{jt} = \frac{1}{M} \sum_{m=1}^{M} \mathbb{I}\!\left(\delta_{jt}^{(m)} = 1\right) \approx P(\delta_{jt} = 1 \mid \text{data}), \]

representing the probability that feature $j$ is associated with trait $t$.

Bayesian MAGMA: Posterior Parameters

In the multivariate setting, we generalize each posterior quantity:

Parameter	Interpretation
$\mathbf{B} = [\beta_{jt}]$	Effect matrix across traits ($j$: feature, $t$: trait)
$\mathbf{PIP} = [\text{PIP}_{jt}]$	Posterior inclusion probability matrix ($j$: feature, $t$: trait)
$\boldsymbol{\Sigma}_b$	Covariance of effects across traits
$\boldsymbol{\Sigma}_e$	Residual covariance among traits

These posterior quantities allow us to identify:

Shared genetic effects (pleiotropy)
Trait-specific vs. shared signals
Cross-trait enrichment of biological or functional sets

Bayesian MAGMA. Study Aim and Design

Evaluate a Bayesian gene-set prioritization approach using BLR within the MAGMA framework.

Simulation study:
- Assessed model performance under varying gene set characteristics and genetic architectures.
- Used UK Biobank genetic data for realistic evaluation.

Comparative analysis:
- Benchmarked Bayesian MAGMA against the standard MAGMA approach.

Applications:
- Applied to nine complex traits using publicly available GWAS data.
- Developed a multi-trait BLR model to integrate GWAS results across traits and uncover shared genetic architecture.

Bayesian MAGMA: Overview

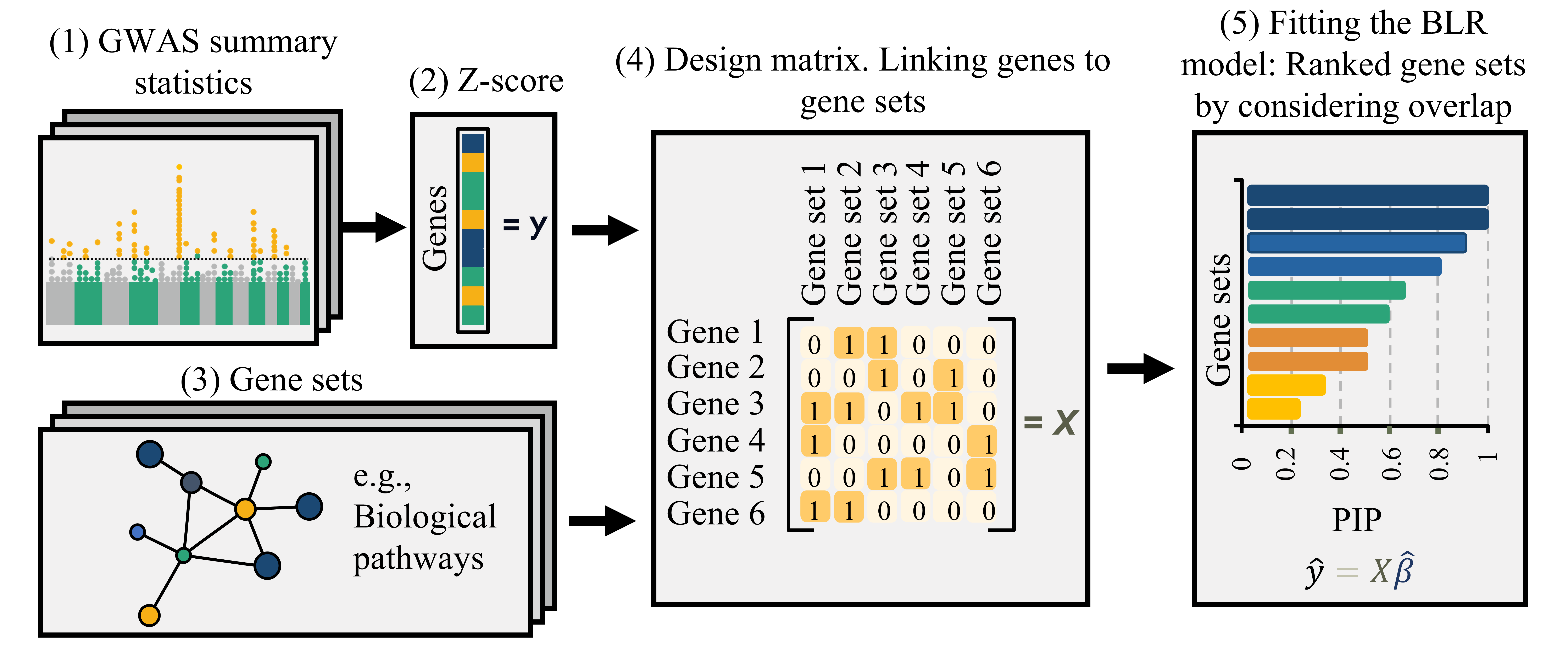
Fits a Bayesian regression model that allows regularization and variable selection
Supports single- or multi-trait a nalyses
Identifies associated features based on posterior inclusion probabilities (PIPs) for the regression effects

Gholipourshahraki et al., 2024

Bayesian MAGMA: Gene-level Statistics

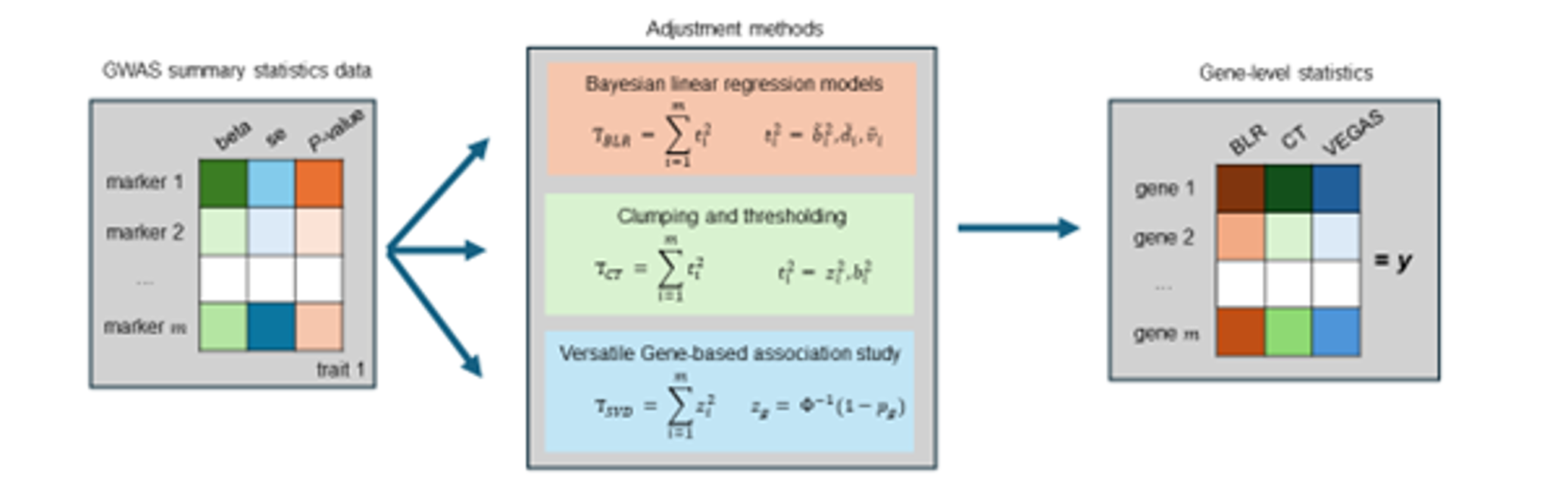
Compute gene-level (or other feature-level) association statistics:

Account for correlation among marker statistics (i.e., linkage disequilibrium, LD)
Different LD-adjustment methods (e.g., SVD, clumping and thresholding, BLR)
The choice of method depends on the quality of the available GWAS summary statistics and LD reference panel

Bai et al., 2025

Bayesian MAGMA – KEGG Pathway

GWAS summary statistics from nine studies (T2D, CAD, CKD, HTN, BMI, WHR, Hb1Ac, TG, SBP)
Gene sets are defined by genes linked to KEGG pathways.
Pathways relevant to diabetes are associated with Type 2 Diabetes (T2D) and correlated traits
Enables identification of cross-disease patterns to better understand comorbidities

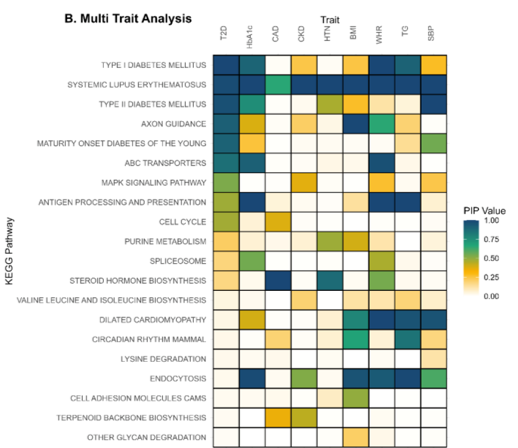
KEGG Pathway Associations

Gholipourshahraki et al., 2024

Bayesian MAGMA – DGIdb

Gene sets are defined by genes linked to the Anatomical Therapeutic Chemical (ATC) classification system using the Drug–Gene Interaction Database (DGIdb)
Drug gene sets relevant to diabetes show associations with Type 2 Diabetes (T2D) and related traits
Novel drug–gene set associations may reveal opportunities for drug repurposing

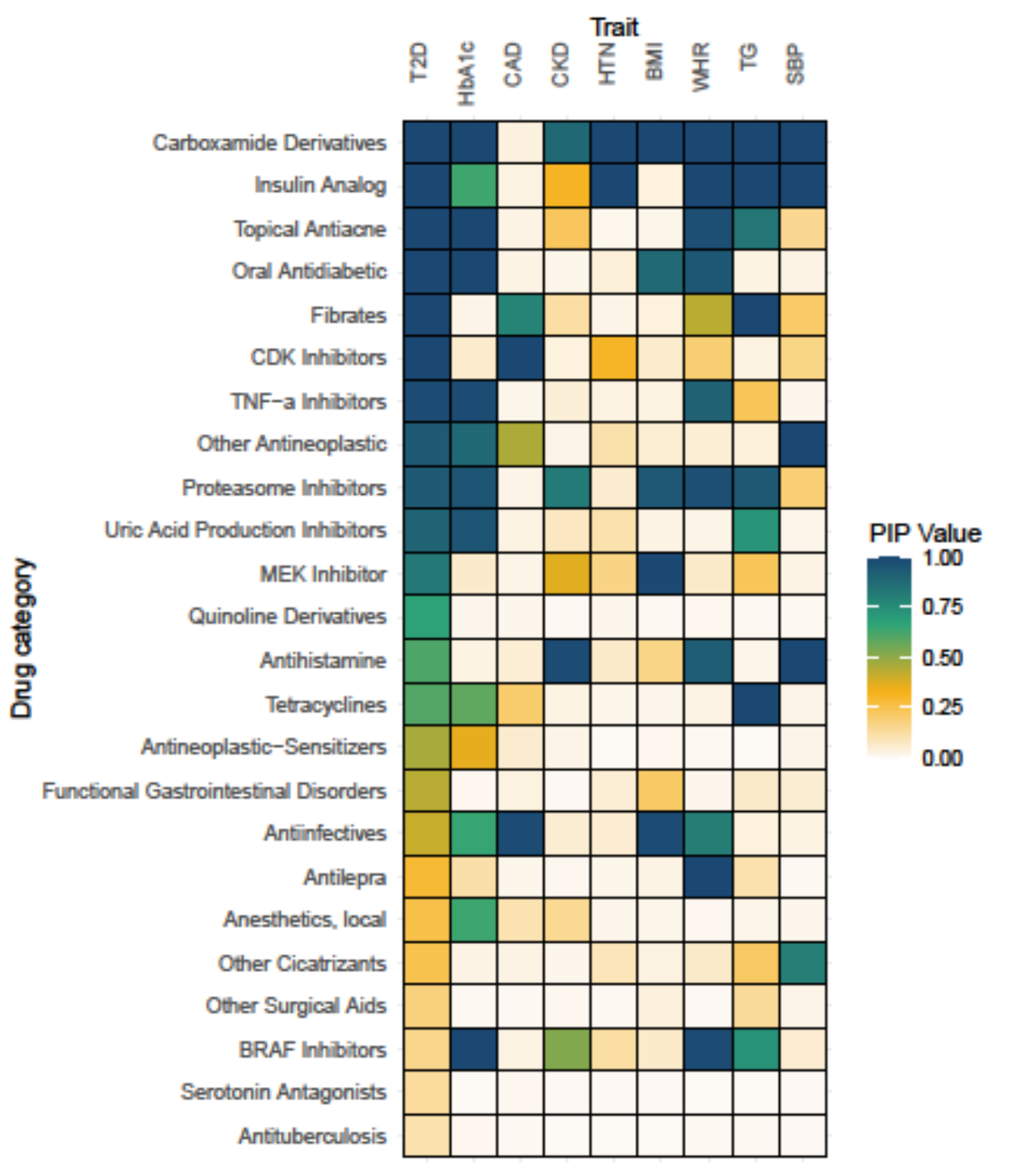
Drug Gene Set Associations (DGIdb)

Hjelholt et al., 2025

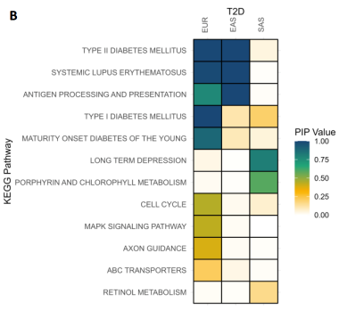
Bayesian MAGMA – Across Ancestries

Gene sets are defined by genes linked to KEGG pathways.
Joint analysis of T2D across three ancestries (EUR, EAS, SAS).
Pathways relevant to diabetes show associations with Type 2 Diabetes (T2D) across two of the ancestries (EUR and EAS).
Comparing these associations helps reveal ancestry-specific biological mechanisms.

Cross-Ancestry Pathway Associations

Summary

Advantages

Incorporates regularization and variable selection via spike-and-slab priors
Accounts for correlated gene sets and traits, increasing power and reducing false positives
Provides posterior inclusion probabilities (PIPs) as interpretable measures of association strength
Flexible framework supporting:
- Single- and multi-trait models
- Integration of diverse genomic features
- Modeling of correlated traits to uncover shared genetic architecture

Limitations

Dependent on the quality and resolution of GWAS summary statistics
Sensitive to biases and incompleteness in functional annotations (e.g., tissue specificity, experimental noise, or overrepresentation of well-studied genes)
Computationally more demanding than standard MAGMA, especially for multi-trait analyses

Future Work

Offers opportunities for hierarchical model extensions (e.g., grouping by genomic or functional layers)
Multi-omics integration to capture regulatory complexity across biological layers
Systematic comparisons with machine learning and deep learning methods to evaluate performance and scalability

References

Sørensen P, Rohde PD. A Versatile Data Repository for GWAS Summary Statistics-Based Downstream Genomic Analysis of Human Complex Traits.
medRxiv (2025). https://doi.org/10.1101/2025.10.01.25337099

Sørensen IF, Sørensen P. Privacy-Preserving Multivariate Bayesian Regression Models for Overcoming Data Sharing Barriers in Health and Genomics.
medRxiv (2025). https://doi.org/10.1101/2025.07.30.25332448

Hjelholt AJ, Gholipourshahraki T, Bai Z, Shrestha M, Kjølby M, Sørensen P, Rohde P. Leveraging Genetic Correlations to Prioritize Drug Groups for Repurposing in Type 2 Diabetes. medRxiv (2025). https://doi.org/10.1101/2025.06.13.25329590

Gholipourshahraki T, Bai Z, Shrestha M, Hjelholt A, Rohde P, Fuglsang MK, Sørensen P. Evaluation of Bayesian Linear Regression Models for Gene Set Prioritization in Complex Diseases. PLOS Genetics 20(11): e1011463 (2025). https://doi.org/10.1371/journal.pgen.1011463

Bai Z, Gholipourshahraki T, Shrestha M, Hjelholt A, Rohde P, Fuglsang MK, Sørensen P. Evaluation of Bayesian Linear Regression Derived Gene Set Test Methods. BMC Genomics 25(1): 1236 (2024). https://doi.org/10.1186/s12864-024-11026-2

Shrestha M, Bai Z, Gholipourshahraki T, Hjelholt A, Rohde P, Fuglsang MK, Sørensen P. Enhanced Genetic Fine Mapping Accuracy with Bayesian Linear Regression Models in Diverse Genetic Architectures. PLOS Genetics 21(7): e1011783 (2025). https://doi.org/10.1371/journal.pgen.1011783

Kunkel D, Sørensen P, Shankar V, Morgante F. Improving Polygenic Prediction from Summary Data by Learning Patterns of Effect Sharing Across Multiple Phenotypes. PLOS Genetics 21(1): e1011519 (2025). https://doi.org/10.1371/journal.pgen.1011519

Rohde P, Sørensen IF, Sørensen P. Expanded Utility of the R Package qgg with Applications within Genomic Medicine. Bioinformatics 39:11 (2023). https://doi.org/10.1093/bioinformatics/btad656

Rohde P, Sørensen IF, Sørensen P. qgg: An R Package for Large-Scale Quantitative Genetic Analyses. Bioinformatics 36(8): 2614–2615 (2020). https://doi.org/10.1093/bioinformatics/btz955

Overview of BLR Models used in Gene Set Analyses

Model Type	Feature Integration	Grouping Basis	Prior Structure	What It Captures
Single-component BLR	Combines all biological features in one model	None	One global variance ($\tau^2$)	All features contribute equally; uniform shrinkage
Multiple-component BLR	Integrates all layers but allows heterogeneous contributions	Learned from data	Mixture of variances ($\{\tau_k^2\}$)	Large, small, and null effect classes
Hierarchical BLR	Groups features by biological structure (e.g., genes, pathways)	Defined a priori	Group-specific mixture of variances ($\{\tau_{gk}^2\}$)	Within-group heterogeneity; enrichment and structured shrinkage
Multivariate BLR	Jointly models multiple correlated traits or outcomes	None or by trait	Shared covariance ($\boldsymbol{\Sigma}_b$) across traits	Genetic/molecular correlations; pleiotropy
Hierarchical MV-BLR	Combines biological grouping and multiple outcomes	Defined a priori	Group- and trait-specific covariance mixtures ($\{\boldsymbol{\Sigma}_{b,gk}\}$)	Shared biological mechanisms across traits and layers

Learning at Different Levels

Model Level	Key Parameters Learned	What They Represent	How They Are Learned	What We Learn Biologically
Effect sizes	$\boldsymbol{\beta}$	Strength and direction of association for each feature	Posterior mean/median given priors and data	Which features drive the outcome
Indicator variables	$\delta_j$ (single trait), $\boldsymbol{\delta}_j$ (multi-trait)	Whether feature $j$ is active (and for which traits)	Estimated as posterior inclusion probabilities (PIPs)	Which features are relevant, and whether effects are shared or trait-specific
Variance components	$\tau^2$, $\{\tau_k^2\}$, $\{\tau_{gk}^2\}$	Magnitude of expected effect sizes; heterogeneity across layers or groups	Inferred hierarchically from the data (via MCMC or EM)	How strongly different groups or omic layers contribute
Covariance components	$\boldsymbol{\Sigma}_b$, $\{\boldsymbol{\Sigma}_{b,g}\}$	Correlation of effects across traits or molecular layers	Estimated from joint posterior	Shared pathways, pleiotropy, and cross-layer architecture

Parameter	Interpretation
\(\mathbf{B} = [\beta_{jt}]\)	Effect matrix across traits (\(j\): feature, \(t\): trait)
\(\mathbf{PIP} = [\text{PIP}_{jt}]\)	Posterior inclusion probability matrix (\(j\): feature, \(t\): trait)
\(\boldsymbol{\Sigma}_b\)	Covariance of effects across traits
\(\boldsymbol{\Sigma}_e\)	Residual covariance among traits

Model Level	Key Parameters Learned	What They Represent	How They Are Learned	What We Learn Biologically
Effect sizes	\(\boldsymbol{\beta}\)	Strength and direction of association for each feature	Posterior mean/median given priors and data	Which features drive the outcome
Indicator variables	\(\delta_j\) (single trait), \(\boldsymbol{\delta}_j\) (multi-trait)	Whether feature \(j\) is active (and for which traits)	Estimated as posterior inclusion probabilities (PIPs)	Which features are relevant, and whether effects are shared or trait-specific
Variance components	\(\tau^2\), \(\{\tau_k^2\}\), \(\{\tau_{gk}^2\}\)	Magnitude of expected effect sizes; heterogeneity across layers or groups	Inferred hierarchically from the data (via MCMC or EM)	How strongly different groups or omic layers contribute
Covariance components	\(\boldsymbol{\Sigma}_b\), \(\{\boldsymbol{\Sigma}_{b,g}\}\)	Correlation of effects across traits or molecular layers	Estimated from joint posterior	Shared pathways, pleiotropy, and cross-layer architecture